Using WebGL to Solve a Practical Problem

An introduction for Dummy Programmers (using the Smith-Waterman Algorithm)

Oct 29, 2019

Some time ago, I was teaching introductory python, and basic browser programming. During this time, I wrote an application that compares pieces of software code and presents their similarity in a force directed and tornado diagram. I ran this software semi-regularly (weekly) and, very early on, a significant problem appeared with my solution.

It took a really long time to solve. A really long time. A painfully long time.

I needed to find a way to speed up the processing.

The points are computer programs, and the orange line represents the progress of a comparison. With 36 comparisons, this takes … long enough that I get bored.

At the time I wrote the tool, GPU processing was hot and everyone was talking about how this was going to speed up everything. No matter what the question, GPU was the answer. This was an obvious avenue of investigation. However, I had decided to write this tool in the browser (legal and ethical constraints), and browsers do not have direct access to the underlying hardware.

So if all the cool kids are using GPUs, and this is written in the browser, and I’m intensely curious …

it looks like I’m learning WebGL and GLSL.

WebGL Demo

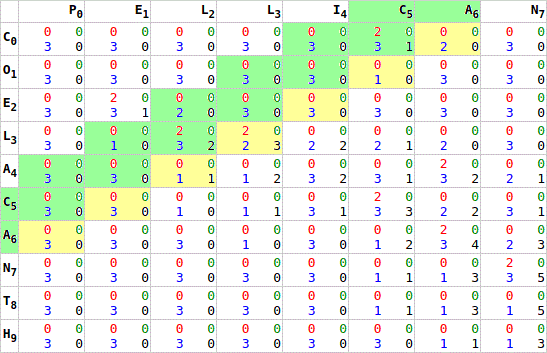
Because WebGL handles 4 memory registers naturally (RGBA), we use those for (four?) memory locations. This also makes…

jefferey-cave.gitlab.io

Since writing M.I.S.S., Google has released tensorflow.js, also other tools like gpu.js and twgl.js are also available. While I chose to directly write in WebGL, the compute abstraction layer offered by these libraries is often useful.
WebGL is not a Compute language … but when has that stopped the adventurous.

Pre-Requisites

Before beginning you should be comfortable with programming. The demonstration is written in vanilla Browser JavaScript, so no particularly advanced techniques are used; however, using WebGL requires switching between two languages, and compiling of code. Web programming does not usually involve those things.

The only programmatic technique you should be vaguely familiar with would be “cellular-automaton”: Conway’s Game of Life is the classic example of this. GoL has been a staple of programming instructors for 50 years because the problem is relatively simple, the solution is complex enough to exercise student skills, and the output is kind of fun.

In addition, I strongly recommend going to the local office supply store and buying a cheap pencil, eraser, and pad of grid paper. Nothing builds understanding like working through problems yourself.

How GPUs Speed Up Processing

GPUs are a completely distinct mechanism from CPUS. CPUs are designed in such a way as to offer many operations to people, and allows you to run them one at a time. GPUs offer fewer operations, but sets them up in a way that you can run a bunch of them simultaneously (parallel processing).

This comes at a couple of different costs to us programmers.

It’s like working on a different computer.
The instructions we write for one, don’t necessarily exist on the other.

That’s annoying, but … parallel processing: as long as they all run the same set of instructions, you can run a calculation a couple of thousand times, but simultaneously. Very simply put:

GPUs do parallel processing of a single function.

Technically, the function is called a “kernel”, in my code I referred to it as a “program”.

Consider the following function:

function MultiplicationTable(size=10){ 
    let table = Allocate2DArray(size);
    for(memLoc.x=0; memLoc.x < list.length; memLoc.x++){
        for(memLoc.y=0; memLoc.y < list.length; memLoc.y++){
            table[memLoc.x][memLoc.y] = memLoc.x * memLoc.y;
        }
    }
    return table;
}

Parallel processing on the GPU is about doing the same action simultaneously. In this case, the multiplication is a process that is consistently the same.

I’m going to just do some basic math: a 10 x 10 array costs us 100 units of processing time.

Now consider the processing using the GPU

function MultiplicationTable(size=10){
    let table = Allocate2DArray(size);
    table = gpu(table)
        .forEach((memLoc)=>{return memLoc.x * memLoc.y;});
    return table;
}

That forEach costs one (1) unit of processing time, no matter whether it is 10x10, or 10000x10000.

I made that code up, it won’t work, but it does give you some idea of what we are trying to work toward. No matter how big we make table it will take 1 unit of processing time.

Using GPUs

GPUs are mechanically different from CPUs.

Because of this mechanical difference, it is useful to think of GPUs as a completely separate computer that you are attached to. Not only do you have separate processing unit (GPU instead of CPU), it also uses separate memory, and a separate instruction set.

These three elements of separation mean there are three major phases that we need to go through to make use of them:

Send the instructions in the GPU space (compilation)
Exchange memory with the GPU space (transfer — read/write)
Execute the instructions (execution)

Managing these three phases are the most difficult and complex part of using WebGL. There are a significant number of details that need to be handled just to exchange information with the other space.

Part of the reason for this is that the G in GPU and WebGL stands for “Graphics”. We are attempting to use something designed for manipulating images, to do general computation. The details that need to be managed revolve around defining elements of an image; this means we need to go through a process of describing our raw numbers in terms of an image.

This is simplified by creating helper functions that will describe our data for us.

psGPU

In WebGL.html, just such a helper class was setup, called psGPU [webgl.html:158]. It has a few functions that abstract much of the configuration away:

addProgram: Compiles and sends a block of GLSL code (as a string) to the GPU space. [webgl.html:384]
initMemory: Creates a hidden image that will act as our processing memory [webgl.html:289]
write: Transfers our memory (UInt8Array) over to the GPU space [webgl.html:254]
read: Transfers our memory back from the GPU space [webgl.html:241]
run: executes the program we compiled [webgl.html:266]

As a novice, these functions became critical to setting up the GPU. I was strongly interested in implementing an algorithm, and the complexities of memory management were acting as a significant distraction to the complexity I wanted to focus on.

`pixel`

At some point, a second helper class was created called pixel. [webgl:96]

The memory that is interchanged through read and write consists of a byte array. The interpretation of an image of as a byte array, calls for a few more helpers. In particular, each pixel of the image is interpreted as 4 bytes, representing the Red, Green, Blue, and Alpha (rgba) values of the pixel. Within the GPU, these values are represented by the type vec4 which is a collection of 4 values (r,g,b,a).

To help maintain consistent naming across the CPU/GPU boundary, the pixel class was created. The pixel class is really just a convenience for mapping the returned UInt8Array to the 4 bytes that represent a given pixel, allowing them to be referred to by the same rgba notation.[webgl:102]

DrawGrid

Probably the most interesting (maybe “useful” is a better word) utility function is DrawGrid. [webgl:828]

Because GPUs are designed to manage images, the only inspection of memory changes that is available is by looking at a picture. Since the purpose of this project has nothing to do with images, colour is not a meaningful representation. This makes debugging … trickier.

To help, DrawGrid does nothing more than render each pixel location as their underlying numeric values. It is roughly equivalent to JavaScript’s console.log, allowing the developer to dump a set of values to a visible location for inspection.

It is most effectively used by placing it (and a break-point) immediately after a kernel run. Don’t forget to comment it out when measuring speed.

Actually Running

Once the helpers are in place, it is a simple matter of defining our processing functions and calling them in the correct order.

Send the instructions in the GPU space
Exchange memory with the GPU space
Execute the instructions

Given the amount of helper code in place, there is not a significant number of instructions left to perform in the actual code portion on the CPU side. All of the really interesting logic should be moved to the GPU; all of the interesting processing should reside in the kernel definitions.

On the CPU side, we send the instructions to the GPU (addProgram), and then repeatedly send notifications to execute the function (run).

The General Problem

Comparing code for similarity is a well solved problem. “Comparing sequences of instructions, while taking into account small variations”, sounds very similar to DNA comparisons.

In the world of genetics, Sequence Alignment algorithms have been around a long time (Needleman-Wunsch dating to about 1970). Comparing sequences of DNA for similarity, while taking into account small variations due to mutation or cross-over is a common goal, is the same problem we are trying to solve. Think of this as a paternity-test for software.

In my case, I reached for a Smith-Waterman comparison.

The best way to understand an algorithm is to solve it with pencil and paper. In this case, I spent a great deal of time with a pencil, eraser, and pad of grid paper from the local convenience store.

Take the names of two animals: coelecanth and pellican.

On the surface, they do not appear similar, however, closer inspection (surprisingly) shows they do align reasonably well:

c o e . l e c a n t h
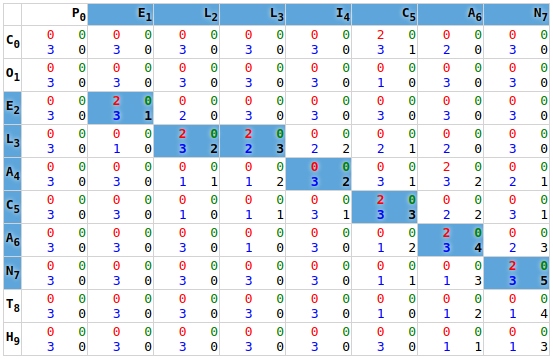
p . e l l i c a n

Programatically we can find this alignment by solving a Smith-Waterman matrix:

In order to understand how the above alignment can be solved mechanically, I recommend following the example given on Wikipedia. I don’t mean go read the Wikipedia page, I mean pull out that grid paper, and reproduce the example for yourself. Solve each step, and verify it against the example. If you made a mistake, spend some time understanding your error, and start over.

When you can solve a Smith-Waterman for yourself, you have proof that you understand it.

While the implementation is discussed in detail below, it it worth having an intuitive understanding of one of the two processes involved; trying to learn both simultaneously is harder. If you are interested in how to implement algorithms on the GPU, already understanding the example algorithm is useful. If you are already a master of the GPU and are interested in how to implement Smith-Watermans, this very basic example may be a good stepping stone.

Put it together

It isn’t easy. Using the GPU requires us to think in parallel, and this requires us think in ways that we aren’t usually used to. Things we take for granted in linear processing aren’t available to us; things we would normally avoid, we accept for the sake of being able to use the tool.

The idea for how to do this actually came from one of my favourite college assignments: Conway’s Game of Life (GoL). In GoL, each life-form location changes its state based on the state of it’s nearest neighbours. This is normally solved in a grid represented with a table of values on the screen.

The key to that statement is that that each automata-cell has a state that is resolved independently of all the others, and based on the values of its nearest neighbours. That pretty much describes the the Smith-Waterman as well. The only real change is that Smith-Watermans only consider the neighbouring cells in the upper-left corner (North, West, and North-West).

These “parent” values need to be calculated prior to being able to calculate values, representing one of the challenges of parallelizing the algorithm: you cannot calculate dependant values in parallel. The first break through mentally was an animated GIF I found online that demonstrated a diagonal parallelization of values in an SW matrix. (the original reference is lost to the recesses of memory now … if you know it, leave a comment)

This was compounded by the fact that I had originally optimised my algorithm for low memory consumption. To do this, I had maximised the early release of the memory associated with a given cell if it was not part of a chain. One of the challenges in using a GPU was determining a way to arrange the memory in such a way that calculations were only performed on elements that have a complete parent set.

Working diagonally, allows us to maintain sufficient parent cells (green) to calculate a number of child cells (yellow) in parallel. Processing this on the GPU means that all of the other cells (white) will be calculated for no reason. A reasonable trade-off.

This focus on optimisation blinded me to the fact that the cost of evaluating a matrix with a GPU is 1 regardless of the size of the matrix. The original speed using CPU calculations required that every cell be evaluated one at a time: width * height processing time. Using the GPU, and calculating all of the elements each time felt like wasteful work, but at some point the realisation it was still only width + height processing time dawned on my dummy programmer brain.

Who cares about wasting a bunch of processing effort when it saves that much time!?

While I’m sure there are efficiencies to be gained, they are insignificant when compared to the speed increases of just evaluating cells needlessly until the entire matrix is solved.

Once this situation is accepted, it becomes reasonable to create the GPU function (or “kernel”) smithwaterman that can solve for an individual 2-D matrix cell [webgl:528]. An initialisation routine was also created which calculates the initial match value [webgl:687].

The first thing to note is the entire program is passed to addProgram as a string. This is to allow the GPU to compile the code, but unfortunately means no syntax highlighting. It also leads to very cryptic messages about invalid syntax. It is recommended that as you make changes, make them small to ensure you can identify where a syntax error was made.

The algorithm itself is very small in its implementation…

Initialise the Memory

Before we can start acting on values, we need to transfer the values to the GPU. While addProgram is used to write the code to the GPU, writing memory is performed by the write function. We start by fetching an appropriately sized array, and then fill only the top, and left portions of the array [webgl.html:735]. This minimises CPU cycles by leaving the iterative portion to the GPU.

The initial Matrix score is done by comparing the extreme North and West values. Matches get a base score of 2 while everything else is set to 0.

Our first GPU task (initializeSpace) is to compare the intersections of these values for matches [webgl.html:687]. For each cell, we lookup the value to the extreme west and north [webgl.html:700], and assign 2 points for a match, or 0 points for a mismatch [webgl.html:707]. This score is stored on the red channel.

It is worth noting that the GPU does its processing in terms of fractional values (float): everything is a portion of 1. So while the scores are intended to be the integer values 0 and 2, these must be consumed as some proportion. The values are actually passed to the function as 0.0/255.0 and 2.0/255.0, making them easily convertible between an UInt8 and float.

This is an important thing to remember. For the purposes of this algorithm:

Everything GPU-side is treating the numbers as floats, but the returned memory is an integer.

Solve the Matrix

Smith-Waterman’s construct a chain of values representing the “best” matches. In this case, “best” is defined as the neighbour with the highest running score.

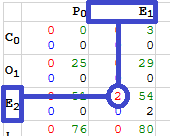
The first step is to look up the nearest neighbours, and this requires us to determine how close those neighbours are. The GPU thinks in terms of fractional values (float), while we are thinking in terms of discrete values (int). We need to calculate the fractional size of a memory location (a pixel) [webgl.html:544]. Once this is done, we can lookup the value of the current cell (here), and its nearest neighbours (nw, n, w) [webgl.html:548].

Once we have identified the critical neighbours, we can begin to assess their values. This is done by checking all three to see which has the highest score, and temporarily storing it on the blue channel [webgl.html:562].

Looking at the nearest neighbours (yellow) we can determine the direction of the match. In this case horizontal (127) is the best match. Values are stored as fractions of 255 (255/2 → 127).

Knowing which score was highest, allows us to determine which direction forms the chain; each direction is tested to see if it forms the desired chain. In the event of a tied score, diagonal matches should be favoured due to, horizontal and vertical matches representing a skip; horizontal and vertical ties can be resolved arbitrarily. Directionality is represented by enumerations of 1-north, 2-west, 3-northwest, and is stored on the blue channel [webgl.html:568].

Knowing the directional of the chain, we can now tally up the running total. The running score of the chain, is added to the local matching score; logically this is done after direction is recorded, however, due to only having 4 memory locations per cell, it is pulled from the temporary value stored on the blue channel before we finalise direction [webgl.html:565]. We also apply a “skip” penalty (-1 points) to chains that had to perform a skip operation (non-diagonal direction) [webgl.html:579].

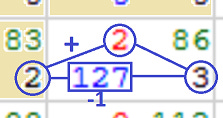
Having identified the parent, we can add the running score, to the local score, and apply any skip penalties. In this case (`2+2-1`), which then gets stored on the current alpha channel.

Once the calculation is complete, the values are stored permanently to the current cell on the alpha channel [webgl.html:584]. It is worth reviewing that there are 4 memory locations per cell, and how we have allocated them:

red: local matching score
green: unused (reserved for future use)
blue: chain direction
alpha: chain score

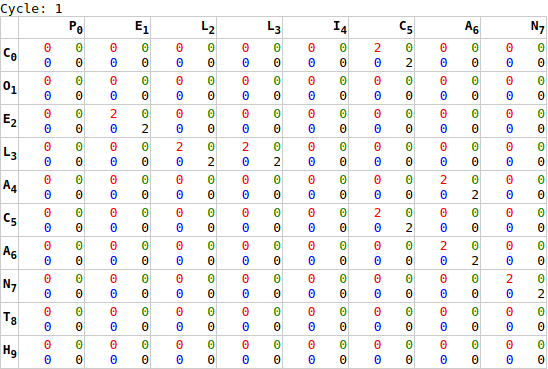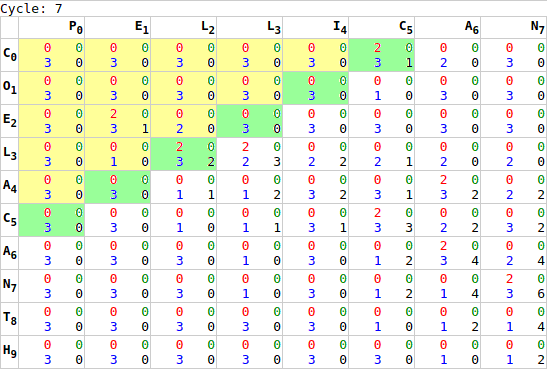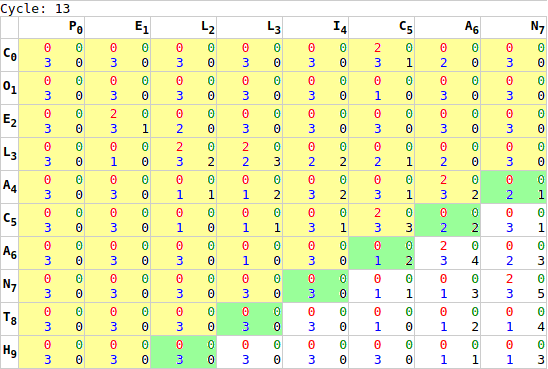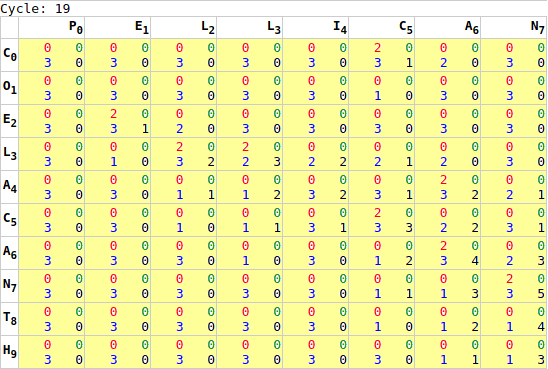
This diagram shows the calculation wave as it moves across the matrix. Green values represent cells with sufficient information to solve, yellow values represent values that have settled into their final state, and white values are ones that are indeterminate. Every cell is calculated on every cycle. Using this pattern, we can reduce the number of required cycles from ``x*y`` to ``x+y``.

As noted earlier, it is not sufficient to execute this process once. While we are calculating every cell’s chain score, there is insufficient information for the last cell to complete its chain calculation until it’s neighbours have completed their calculation. To resolve this, we run the GPU processing multiple times: first calculating the worst-case number of cycles required [webgl.html:518], and then sending processing signals to the GPU a loop [webgl.html:752]. Each iteration of GPU processing moves the “wave” of completed calculations forward one step.

Once this loop completes, and the tip of this wave reaches the bottom-right of our matrix, the first phase of the calculation is complete. Most importantly it was completed in x+y cycles, rather than x*y cycles. While the test samples are too small to take accurate readings (1ms resolution in most browsers), the animals sample went from 10ms to under a millisecond, while the lorem sample went from 5.5 seconds to about 1 millisecond, no initial readings were taken for identical, longchain, or gilbertsulivan [webgl.html:477].

Even accounting for significant measurement error, this is a significant improvement!

We can see a significant improvement in speed in just the first 30 seconds of processing.

Conclusion

I can no longer find the source, but one of the best over views of the GPU on the web was from a video of a conference talk that ended with

If this feels like a dirty hack to you, that’s because it is.
— if you know the video, please leave a comment

Some of this definitely has the feel of a dirty hack, for example, working around all the references to RGBA feels weird. WebGL was designed for graphics, not a computation. For the adventurous, this lends a sense of excitement and challenge.

I find this takes me back to my (very brief) days of working in `C`, where memory manipulation is a little closer at hand. Conforming to vec4 memory (rgba) really encourages you to think of new ways of using (and abusing) the way you use memory, or reusing memory, or squeezing that extra bit of information into an incompletely used byte (most of which has been refactored out of the example).

While I have loved Conway’s Game of Life for decades, I never thought I would find a practical purpose for cellular automatons. Having noticed the similarity between this problem and GoL, I now want to revisit a personal attempt at a JavaScript implementation of aerosolized particulate dispersion models (mine has gone missing, this one is pretty cool).

Lastly, the most educational part of this for me was the value of pencil and grid paper. A lot of debugging revolved around solving the grid with a pencil and then comparing the resulting manually solved matrix to the program’s solution.

Solving Smith-Waterman’s by hand is also like doing a giant Sudoku or Crossword… kind of fun.

Next Steps

Open in the browser
Hit F12
Insert a Break-point
Start stepping through code

In this case, I’d actually suggest saving a local copy first to allow you to make minor changes to see the effect.

The performance gains I see by implementing the algorithm on the GPU were significant: approximately 5000 times in terms of speed. However, the more I ponder the problem, the more ways I see to improve it.

On the other hand …

This tool was written as a personal utility to meet personal needs. Until such time as there is more interest in M.I.S.S., there is likely little reason to implement performance gains.

Its fast enough… for now.

Looping

I suspect my calling of run in a loop is inefficient. Likely, it would be better to implement the loop as part of the GPU code. However, there are two reasons I did not do this:

The current implementation allows for periodic reading of the data, allowing for progress bars in the visualisation (orange connectors).
Input and Output memory is declared prior to execution. In the helper functions, input memory and output memory are swapped after every run. I don’t know how to do this within the context of a single execution.

Neither of these issues seem insurmountable.

Chain Resolution

Smith-Waterman calls for two phases

Build the chains
Resolve the chains

This article intentionally ignores the second phase of a Smith-Waterman; the code that reads the chains back off the memory. The current implementation in M.I.S.S. uses pure CPU JavaScript to resolve the chains. However, a recent discussion in the office got me re-thinking about how that was done, and inspired me to rewrite the chain resolution function to use the GPU more.

I encourage readers to have a look at the GPU function chain [webgl.html:588] to see its implementation. It uses very similar techniques to those already discussed [webgl.html:763].

Memory Consumption

Building a 2-D matrix in memory means height times width. That is going to grow quickly depending on your inputs. Also, as the number of token grows, there is a risk that the numbers that represent them will exceed 65535 (2-bytes).

One of the initial validation tests I had for the code was to do a comparison between the genomes of E.Coli and Y.Pestarius [bigcompares.zip]. Unfortunately, that eats up memory, and an 8TB array exceeds my laptop’s capabilities.

I would love to see an implementation that cuts the giant matrix into a series of smaller ‘tiles’ (16000x16000 for about 2GB?). This would ensure that they never consume more memory than is available, and never generate a token identifier greater than 2-bytes.

Tokens could be mapped to an index not exceeding UInt16, for the given tile. The tiles could be solved for independently (in parallel if you have more than one GPU), storing only their internal chains and edges. The edges could then be “stitched” together during chain-resolution.

It’s an interesting idea, and I’d love to see someone run with it…

Jefferey Cave

Discussion about this post